“There is something of greater significance than the allure of captivating discoveries, and that is comprehending the very methodology employed in their creation.” – Leibniz, the eminent philosopher and mathematician.
The first-ever image of a black hole, captured on April 10, 2019, served as definitive evidence supporting Albert Einstein’s groundbreaking theory of general relativity. The confirmation of black holes’ existence in the cosmos, however, is not the sole or direct proof of the theory. The credit for this validation goes to an exploratory expedition led by the renowned astronomer Arthur Eddington, which took place exactly one hundred years ago on May 29, 1919. During this expedition, a solar eclipse was meticulously analyzed. Today, as the scientific community commemorates the centennial anniversary of the verification of the general theory of relativity, I take great pleasure in presenting a scientific article that provides a comprehensive analysis of both the special and general theories of relativity, specifically tailored for non-specialist readers.
During the period spanning the mid-nineteenth century to the early twentieth century, a perplexing set of inquiries arose, causing considerable consternation among physicists and mathematicians. These quandaries were referred to by the esteemed physicist Lord Kelvin as inconsequential ‘clouds’ looming on the horizon. What led this eminent scientist and his supporters to believe that physics had reached a state of absolute perfection? If one were to peruse a specialized physics textbook, it would reveal approximately 1,000 pages elucidating natural phenomena prior to the twentieth century. There is no need for alarm, for these 1,000 pages, along with countless other books expounding on natural phenomena, constitute the material covered in public education and the first year of university studies for non-science students. Many of us have struggled through Newton’s ingenious concepts while grappling with equations of motion and vector calculations. Take pride in how far you have come in comprehending physics. You have delved into what we physicists, as well as students of natural sciences and engineering, commonly refer to as “classical physics,” which elucidates various natural phenomena, including the movement of bodies, fluids, heat, sound, light, electricity, and magnetism.
In most books that aim to simplify the theory of special and general relativity, a significant part is dedicated to explaining the fundamental principles of astronomy. This typically involves discussing the influential giants upon whose shoulders Newton built his own work, such as Copernicus, Tycho Brahe, Kepler, and Galileo. Subsequently, considerable attention is devoted to elucidating Newton’s groundbreaking contributions to classical physics, specifically his pioneering efforts in redefining the concept of space from absolute to relative. However, I propose a shift in the narrative direction by approaching it by touching upon the concept of ‘light.’ This alteration is motivated by the following reasons:
Firstly, it is universally recognized among physicists that the pursuit of understanding the nature of light lies at the heart of intellectual dilemmas in physics.
Secondly, the enigma behind numerous natural phenomena we observe today, such as the blue hue of the sky, rainbows, and the aurora borealis, can be attributed solely to the properties exhibited by light.
Thirdly, the very foundations and principles that underpin the technology we rely on today, encompassing everything from our indispensable electronic devices to the mechanisms employed in capturing images of galaxies, stars, and black holes, owe their existence to the unique properties and nature of light. Light transcends being a mere ray; it serves as an information-transmitting medium.
Lastly, and of utmost significance, the seeds of relativity sprouted within Einstein’s mind from a moment of creative and imaginative contemplation. He pondered what a beam of light would appear like if he were to race alongside it at the same velocity. I seek to introduce the concept of relativity in homage to Einstein’s pensive inquiry, recognizing that at the time, the answers were minute in comparison to the immense magnitude of the questions.
What is light?
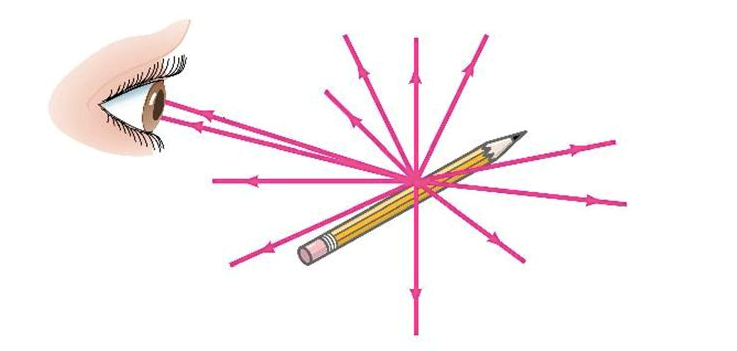
The significant work in unraveling the nature of light, through the lens of the scientific method, can be attributed to the pioneering work of the esteemed Arab and Muslim scholar, Al-Hasan Ibn Al-Haytham. He embarked on an unprecedented scientific endeavor by meticulously analyzing the process of vision. Indeed, Ibn Al-Haytham’s groundbreaking insights revealed that light emanates from various points on objects, traverses a linear path, and ultimately reaches the eye, where it is interpreted by the brain in the form of visual images. This systematic examination of optical phenomena, documented in his renowned work, the Book of Optics, also encompassed the study of light’s properties, such as reflection and refraction, employing lenses. This empirical exploration of optics paved the way for astronomers to delve into the movement of celestial bodies, planets, and stars through telescopes. The profound impact of these astronomical observations played a pivotal role in dismantling the long-standing notion of Earth’s centrality within the universe.
René Descartes was the first to describe light as a wave, although his explanation was rather limited. It was the scientist Hooke who further posited that light represents the vibration of a medium through which the wave propagates. Notably, Hooke introduced the concept of “the medium and mediator” for the first time, referring to the material entity that transmits the wave. Subsequently, the scientist Huygens designated this medium as “the ether” and defined light as a disturbance in the ether that propagates in the form of a wave. However, the eminent scientist Isaac Newton proposed a fundamentally different notion, asserting that a light source emits an abundance of minuscule particles devoid of weight, which travel in straight lines even through a vacuum. This theory is widely known as Isaac Newton’s corpuscular theory of light. The divergence in conceptualizing the nature of light engendered a significant question: Is light characterized as a particle or a wave?

Newton’s contributions surpassed those of Huygens in terms of evidence and explanation. Newton elucidated that white light is, in fact, a composite of multiple colors known as the seven colors of the spectrum. This can be observed in the captivating natural phenomenon of the rainbow, where white light is dispersed and analyzed into its constituent colors using a prism. Conversely, if an opposing prism is employed, the colors recombine, forming white light once again. However, Newton’s corpuscular theory did not fully account for why light undergoes refraction in the manner observed. In response, Huygens ingeniously utilized Newton’s weightless particles as the medium of the ether, asserting that light is nothing more than disturbances in the ether that propagate as spherical waves. Huygens’ insistence on the existence of the ether stems from our understanding of light’s properties, particularly the explanation for the refraction of light based on the differences in density between substances. For instance, when we immerse a pen halfway into a glass of water, it appears to be broken when viewed from above. This phenomenon arises due to the disparity in density between water and air. If we replace the water with other transparent substances such as oil, a sugar solution, or a transparent alcohol solution, the pen will similarly appear distorted, albeit at different angles depending on the refractive index of each substance.
Unfortunately, Huygens’ wave theory of light did not initially gain significant traction, possibly due to the immense influence of Newton’s reputation. However, a pivotal development occurred when the physicist Thomas Young conducted a groundbreaking experiment known as the “double-slit experiment.” This experiment involved positioning a light source behind a barrier containing two narrow slits, with a screen placed in front. As light passed through the slits, the resulting waves superimposed and created alternating dark and light bands on the screen, as depicted in the accompanying diagram. This phenomenon can be readily explained by drawing an analogy with water waves. The two slits give rise to two sets of waves. When the peaks of a wave from one slit align with the peaks of a wave from the other slit, a phenomenon called “constructive interference” takes place, resulting in bright bands. Conversely, when the peaks of a wave from one slit align with the troughs of a wave from the other slit, a phenomenon called “destructive interference” occurs, leading to dark bands. The double-slit experiment conclusively demonstrated, through empirical evidence, that light behaves as waves, thereby effectively disproving the particle theory of light.

But if light is a wave, what is it that undulates?
When you take your child to a serene lake on a beautiful spring day and place a little paper boat on its surface, you can create ripples by gently disturbing the water. These ripples, in essence, generate vibrations in the water. But what exactly is vibrating in this scenario? In reality, it’s the water molecules themselves that are not moving extensively but rather following the motion of your hand. As you press your hand into the water, the water molecules in that region become compressed. Through collisions with neighboring molecules, this compression is transmitted, resulting in a rippling motion that propagates as waves, moving away from the source of disturbance. It is important to note that it is the wave itself that moves through the water, not the water molecules as a whole. If the water molecules were the ones primarily moving, we would observe the boat shifting in response to the water waves. However, this is not what we typically notice. Instead, we observe the paper boat being influenced by the rippling motion of the water, causing it to move. The waves, on the other hand, continue to propagate and move away from the boat until they eventually dissipate or disappear.
The dilemma here lies in the fact that waves cannot be created without a medium through which they can undulate. This applies even to sound waves, which require a physical medium. Due to variations in the density of different media, the speed at which sound waves propagate also differs.
“When considering human history as a whole, the indisputably most significant event in the nineteenth century is Maxwell’s discovery of the laws of electrodynamics.” – Richard Feynman
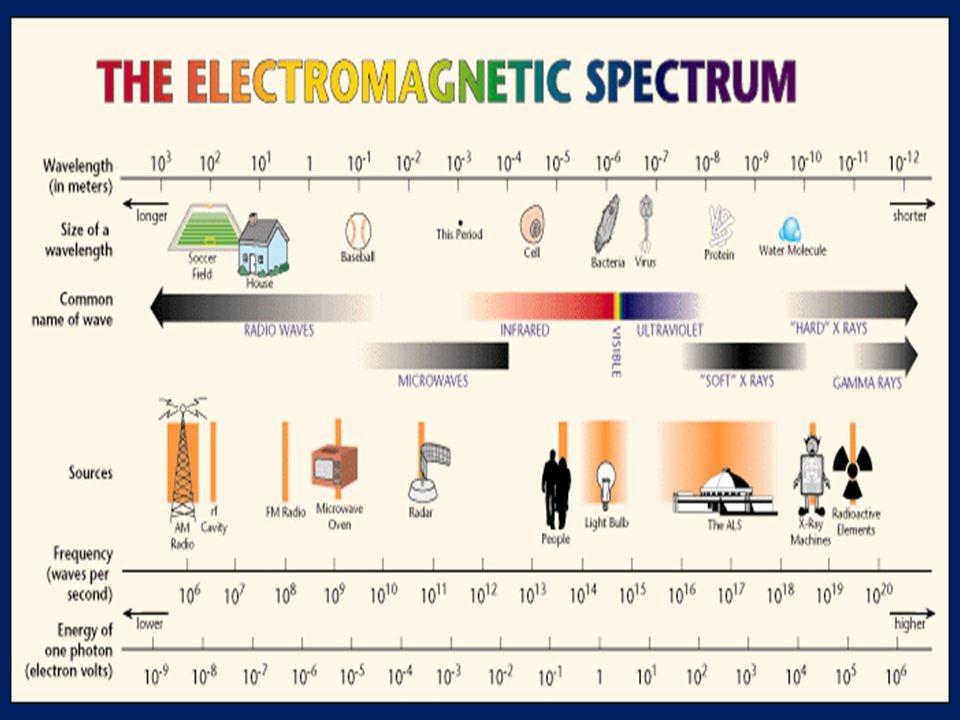
In 1856, the renowned scientist Maxwell published his work on the theory of electromagnetism. Building upon the research conducted by Faraday, Maxwell developed a dynamic theory that described the electromagnetic field. He proposed that light consists of dual waves of electricity and magnetism, perpendicular to each other, traveling in an alternating manner through infinity. In his final paper, Maxwell presented a set of 20 highly complex molecular differential equations, which provided a complete mathematical description of the electromagnetic phenomenon. Maxwell’s primary objective was to address the question of how light waves propagate in a vacuum. However, his theories remained unverified experimentally until another scientist named Hertz, whose name is now known thanks to its association with the unit of wave frequency, unraveled the mysteries of electromagnetic waves. Hertz not only confirmed Maxwell’s predictions but also expanded humanity’s understanding by discovering various types of electromagnetic waves. It became apparent that visible light, which was previously thought to encompass all that is known, is merely a fraction of the electromagnetic spectrum. The range of visible light spans from approximately 400 nanometers (violet color) to 700 nanometers (red color). Beyond the red end of the spectrum lie wavelengths that are invisible to the human eye, such as infrared radiation, radio waves, and microwaves. Similarly, wavelengths shorter than violet (ultraviolet rays) are also undetectable to the naked eye. These include X-rays, alpha particles, beta particles, and gamma rays, which can be harmful to living tissues.
Upon validating Maxwell’s theory and determining that the speed of electromagnetic waves is constant, a contradiction arises between Maxwell’s theory and Newton’s theory, which posits the absence of an absolute reference frame. To reconcile the two theories, the concept of an ether, a material medium with peculiar physical characteristics (invisible, massless, incompressible, and extremely dense), is reintroduced. This ether serves as the absolute reference frame for all motion in the universe and consequently influences the speed of light propagation. Imagine standing on the edge of a tall hill on a windy day. As the strong wind blows against you, you experience a sensation akin to galloping into the wind, feeling an increase in speed that almost resembles flying. Conversely, if you were to run against the wind, you would encounter significant resistance, potentially even coming to a halt due to the opposing force. Similar dynamics apply to light. Its velocity will be influenced by the movement of the Earth, causing fluctuations in its speed, either an increase or a decrease.
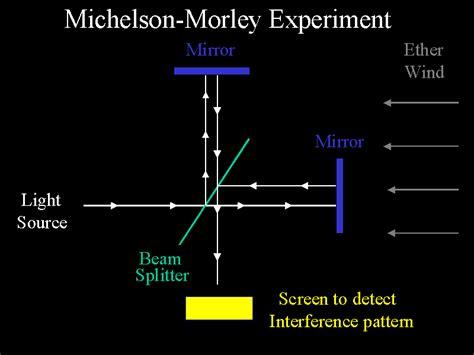
Numerous experiments were conducted to investigate variations in the speed of light, with many of them relying on astronomical calculations. Notable experiments include the Romer experiment and the Fizeau experiment, which was the first in-vitro experiment. However, the most significant and precise experiment in this regard was the Michelson-Morley experiment. The Michelson-Morley experiment aimed to detect changes in the speed of light relative to the ether by employing an interference-based measurement. In this experiment, light from a source was split into two beams using a semi-silvered mirror. The two beams of light traveled at right angles to each other and were subsequently recombined into a single beam after encountering the semi-silvered mirror. If there were discrepancies in the speed of light along these two directions, it would imply that the crests of the waves in one beam coincided with the troughs of the waves in the other beam, resulting in their cancellation. However, the stability of the interferometer used in the experiment demonstrated that the speed of light remained constant. The experiment was repeated in different regions and seasons to examine potential variations caused by etheric winds, yet the results consistently supported the conclusion that “the speed of light is constant.” Although the Michelson-Morley experiment did not achieve its original goal of confirming changes in the speed of light, it serendipitously succeeded in proving the constancy of light’s speed. Moreover, it measured this speed with exceptional accuracy, determining it to be approximately 300,000 km/s. Due to the significance of this experiment, Michelson was awarded the Nobel Prize in Physics in 1907.
What does this big number mean?
The speed of light allows it to traverse the Earth approximately seven and a half times within a single second. This characteristic is the reason why we employ the unit of measurement known as a light year when quantifying vast distances between stars and galaxies.
The constancy of the speed of light presents two potential implications:
- If the speed of light is constant, it would imply that the Earth is motionless in relation to the ether. However, this contradicts well-established astronomical laws that have been validated through experiments.
- Alternatively, the concept of the ether’s existence becomes untenable, which would invalidate the revision of Newton’s laws.
The perplexing contradiction prompted scientists to undertake extensive efforts in order to reconcile the concept of the ether. Among these endeavors, the contributions of physicists Lorentz and Fitzgerald proved to be the most accurate and closest to elucidating the reason behind the constant speed of light. They proposed that the Earth is not stationary but rather undergoes a physical contraction. Their calculations, known as the ‘Lorentz-Fitzgerald contraction,’ precisely determined the extent of this contraction. In their explanation, they attributed the compression to a dynamic transformation occurring within the atoms of the Earth, signifying a change in the physical properties of matter.
The Kelvin clouds, which were previously considered insignificant, have now transformed into storm clouds ravaging the skies of natural sciences and philosophy. Intense debates surrounding these issues took place in Europe, particularly within the Prussian and German empires. One prominent figure who voiced strong criticism towards Newton’s works and the concept of the ether was the philosopher and physicist Ernst Mach. Mach expressed his dissent in his book titled The Science of Mechanics. However, what set Einstein apart was his profound engagement with formal logic in his thinking process.
“The theory of special relativity is steeped in contradiction.” – Albert Einstein
The stage is now for Einstein
The dilemma arises from examining the contradiction between Maxwell’s theory and Newton’s theory. The absence of a new scientific mechanism to test this contradiction is what prevents a resolution. Physicist Albert Einstein was among the great minds who introduced a groundbreaking idea: the absence of ether. According to Einstein, electromagnetic waves do not require a medium for transmission; they are a self-contained network of connections. This concept stems from the understanding that space is not an absolute reference but rather a relative framework dependent on the observer’s perspective.
Let’s adopt Einstein’s perspective and consider the implications of a constant speed of light:
Imagine a scenario where I engage in a race with a beam of light. No matter how much I increase my speed, the difference between my velocity and the speed of light will always remain the same. I will observe that the beam of light continues to move away from me, instead of me approaching it.
What is this madness? What does it mean?
The upcoming lines will contain a significant amount of chaos, so I will use a hypothetical thought experiment to illustrate the point:
Let’s consider a scenario involving two twin brothers, Ahmed and Khalid, who share a passion for adventure and decide to challenge each other to a car race. Ahmed takes an initial lead of five seconds before Khalid begins his race. According to Newton’s laws of motion, regardless of how fast Ahmed’s car may be, Khalid will eventually catch up to him. This occurs when Khalid’s speed or acceleration surpasses that of Ahmed’s car, after a certain distance and time. Now, imagine that Sarah, their sister, is observing the race and decides to shoot a laser beam across their cars. Khalid, driven by his daring nature, entertains the idea of catching the laser beam. In order to achieve this, he would have to increase his speed to the maximum possible. However, even if his car possessed exceptional specifications, such as the ability to travel at 95% of the speed of light, he would be unable to catch the beam of light. This is the case even if Sarah, Ahmed, and Khalid were positioned in such a way that they were approaching the beam of light. According to Newton’s laws, Sarah would measure Khalid’s speed as follows:
Resultant velocities = speed of light + speed of Khalid’s car
= 300,000 km/s + 285,000 km/s (95% of the speed of light)
= 585,000 km/s (this is an amount that exceeds the speed of light)
Consequently, Sarah held the belief that her brother Khalid had successfully caught the beam of light. This conviction arose from the fact that she measured the event from her own frame of reference, which was the starting point of the race. In contrast, Khalid’s frame of reference was his moving car, which was traveling at a velocity equal to 95% of the speed of light. From Khalid’s perspective, however, he did not manage to capture the beam of light. This is because the speed difference between Khalid’s car and the speed of light remains constant, owing to the inherent and unchanging nature of the speed of light itself, which is universally recognized to be 300,000 km/s. If Sarah’s interpretation were accurate, it would imply that the speed of light is variable. Yet, as previously established, the constant speed of light stands as an indisputable fact.
Therefore, Einstein developed the hypotheses of the special theory of relativity, building upon two fundamental principles:
- All laws of physics hold true regardless of the frame of reference in which they are observed.
- The speed of light remains constant in a vacuum and is unaffected by the motion of the source or the observer.
These two hypotheses led to the abandonment of the concept of the ether, which had been previously proposed. The notion of the ether exists today only in the misguided statements of certain radio broadcasters who inaccurately claim, “We transmit to you, our valued listeners, through the waves of the ether from our station.”
Reference frames:
In nature, describing any form of motion requires a frame of reference (space and time). When arranging to meet a friend, you must communicate the specific location and time of the rendezvous; otherwise, you will never converge. However, in the domains of physics and mathematics, a higher level of precision is necessary to delineate location. Therefore, we employ a three-dimensional representation (length, width, and height) using Cartesian axes. Inertial reference frames are the frames of reference that adhere to Newton’s first law, wherein objects move without inertia, signifying a state of consistent stability or continuous motion at a constant velocity. To illustrate this concept more clearly, let’s consider a scenario: Imagine a person driving a car, and a coin accidentally falls from their possession. From the perspective of a passenger within the car, the coin falls vertically. However, for an observer situated outside the car, the coin descends in a curved trajectory due to the car’s movement relative to the ground.
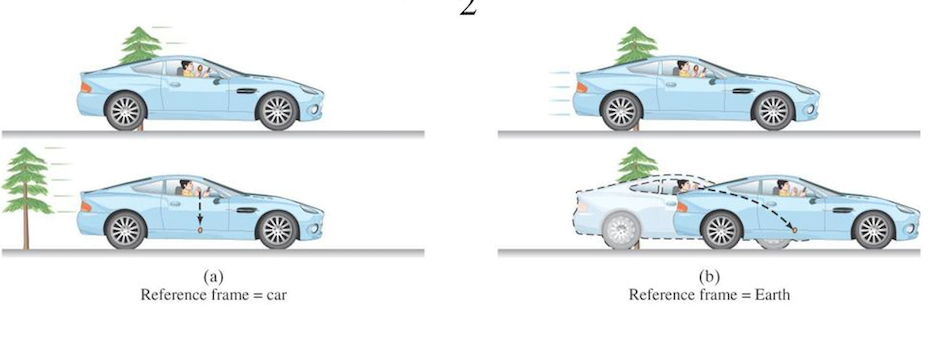
Both Galileo and Newton recognized the principles of relativity pertaining to different frames of reference. The equations that elucidate the same event in two distinct frames of reference are referred to as the Galilean Transformation of coordinate equations. The first assertion put forth by Einstein stands as an axiom within the realm of mechanics. In the accompanying picture, the vertical descent on the left side accurately adheres to the laws of basic mechanics, but it is crucial to emphasize that its accuracy is contingent upon its frame of reference (the moving car). Conversely, the curved descent depicted on the right side of the picture also aligns with the laws of elementary mechanics, but it is imperative to underscore that its accuracy is tied to its frame of reference (the Earth).
In short, relativity can be understood as follows: Different observers will measure or observe different quantities, yet the fundamental laws of physics remain consistent. This serves as an explanation for the first hypothesis.
What limitations prevented Galileo’s equations from accurately describing relativity?
In Galileo’s and Newton’s mechanics, objects were perceived to move at varying speeds due to the assumption of absolute space and time. In contrast, the speed of light is found to be constant. This discrepancy led to the realization that space and time must be relative rather than absolute, and this is where Einstein’s genius became evident.
Results of special relativity:
1. Length Contraction
The constancy of the speed of light implies that other physical quantities related to speed, such as distance and time, are variable. In classical physics, speed is defined as the rate of change of distance with respect to time, where changes in speed can be described as acceleration or deceleration. Physically, distance refers to the three spatial dimensions in which we exist, while time, although its true nature remains elusive, is measured by the Earth’s movement, including its rotation on its axis and its orbit around the sun. Our connection to Earth has led us to believe that space and time are absolute, meaning that they remain constant regardless of our motion. In this perspective, we would perceive an explosion on Mars at the same moment, and any movement in the universe could be calculated using simple algebraic calculations based on factors such as speed, distance, and time, relying on Newton’s laws of motion. However, the constant speed of light serves as an absolute reference for motion, revealing that the dimensions of space and the measurement of time differ for different observers depending on their respective frames of reference. In order for motion to remain consistent, there must be changes in the dimensions of space (expansion or contraction) as well as in terms of time (dilation or contraction). This concept is reminiscent of the “Lorentz-FitzGerald contraction” proposed by Lorentz and FitzGerald, who attributed the constant speed of light to a physical compression of the Earth. However, it should be clarified that this contraction does not result from atoms being compressed, but rather from a compression of the spatial dimensions themselves. This phenomenon is known as “length contraction.”
Let’s consider the thought experiment involving the twin brothers, Ahmed and Khalid, at a train station. Suppose Ahmed is aboard a train moving at a speed close to the speed of light. Due to a mechanical issue, the train does not stop or decrease its speed at the station. Inside Ahmed’s train cabin, there is a sign with dimensions of 100 cm in length and 150 cm in width. If we were to ask Ahmed about the dimensions of the sign, he would perceive and measure it as having a length of 100 cm and a width of 150 cm from his frame of reference on the moving train. However, Khalid, who is waiting at the train station, would observe and measure the sign to have a length of 100 cm and a width of 65 cm. This difference in measurements arises because the dimension that experiences contraction is the one aligned with the direction of movement. In this case, the width of the sign is the dimension that shrinks, as it is horizontal relative to the train’s motion. If the train were traveling at an extremely high speed in a vertical direction, the dimension that would contract would be the length instead.
Relativity comes into play here. Both Ahmed and Khalid’s answers are correct, as each observer “observes/measures/watches” according to their respective frame of reference. Ahmed, who is on the train moving at a speed close to the speed of light, measures using his own frame of reference (the space of the moving train at a speed close to the speed of light). On the other hand, Khalid measures the width from a different frame of reference, resulting in a slightly smaller measurement (He is standing still while observing the train moving at a speed close to the speed of light).
2. Time Dilation

What is time?
This question has long troubled philosophers, intellectuals, natural scientists, and religious scholars throughout history, and it continues to trouble them. Poets have sung about time, lovers have wished for it to stop, sinners have longed to return to the past, and dreamers have yearned to travel to the future.
In classical physics, particularly in Newtonian physics, time was considered absolute. According to this view, if there was an explosion on the sun, its effects would be seen instantaneously. Time was seen as a linear journey, progressing unidirectionally from the past, through the present, and into the future. This conception of time left no room for turning back. The renowned German philosopher Immanuel Kant referred to the paradoxes associated with this notion of time as “the contradiction of pure reason.” If time is eternal and the universe is absolute, why did events that are yet to occur not already happen in the past?
It is said that Einstein once conducted a thought experiment shortly after leaving his work at the patent office. He gazed at a clock tower in the city of Bern and imagined himself traveling away from it at the speed of light on a train. In his imagination, time appeared to freeze. “Time would stop,” he contemplated. Reflecting on this incident, he remarked, “It was like a storm that swept through my mind.”
We have previously established that the constant speed of light serves as an absolute reference for motion. This implies that the changes occur in the dimensions of both space and time. We have learned that lengths contract in the direction of motion at the speed of light, and in order for the mathematical and physical relationships to remain consistent, time must expand. In other words, time passes more slowly. This phrase does not imply a sense of boredom, but rather indicates that the true measurement of time differs for objects traveling at the speed of light.
Returning to our previous thought experiment involving the twins Ahmed and Khalid, let us consider the scenario where Khalid is waiting at the station for his brother Ahmed, who is scheduled to arrive at two o’clock in the afternoon. However, due to a malfunction in the train, it does not stop. At exactly two o’clock, Ahmed, who is on the train moving at a speed close to the speed of light, asks us: “What time is it?” He glances at his watch, which displays 1:57 minutes. Ahmed’s watch is functioning properly and has not been affected by any damage. We are aware that watches are merely instruments for measuring time. For Ahmed, the discrepancy in time arises because within his frame of reference (moving in space at a speed close to the speed of light), time expands and “flows” at a slower pace. On the other hand, Khalid, who remains stationary on Earth, experiences time in the usual manner within his frame of reference. Both Ahmed and Khalid accurately and correctly measure time based on their respective frames of reference.
I acknowledge that this statement may seem illogical since it challenges the notion of absolute time, our familiar earthly time. However, I will present the evidence supporting it:
If the sun were to suddenly vanish, we would witness its disappearance after a duration of eight and a half minutes. What we consider as “the moment we observe the sun’s disappearance” is actually in the past for the sun. In our present on Earth, the sun has already transformed into a neutron star, and we would witness this transformation another eight minutes later, which we perceive as a “future moment.” These are not fictional ideas but rather conclusions derived from the principles of special relativity. This is why Einstein famously remarked, “I have set a clock everywhere in the universe.”
The relativity of time remains a challenging concept to grasp, and Einstein devised a thought experiment called the twin paradox to help people understand it better. Let’s revisit the twin brothers Ahmed and Khalid. Suppose Khalid, the adventurer, embarks on a space journey to a distant star and returns to Earth aboard a spacecraft traveling at a speed close to the speed of light. The twins bid farewell to each other at the age of 20. From the perspective of relativity, time passes more slowly for Khalid due to his high velocity. If his round trip takes one year according to his frame of reference—moving at a speed near the speed of light—Khalid would return to Earth at the age of 21 according to the spaceship’s clock. However, he would be astonished to find his twin brother Ahmed now at the age of 40. There is no paradox here; it is simply a consequence of Ahmed experiencing time within a different frame of reference, where time does not dilate like it does for Khalid. Earth time, at relatively low speeds, imposes certain limitations upon us due to our connection to the Earth.
3. Mass and energy are two sides of the same coin:
In every internet search related to Einstein, you will invariably come across the image of the equation displayed above. Let us explore its story together. In physics, there is a crucial fact: all laws are interconnected, forming a cohesive framework, as illustrated in the approximate figure below:
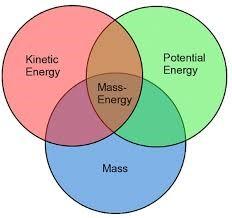
It is not possible to study a physical law in isolation from the rest of the laws. In the laws of motion, when a body moves, it covers a certain distance at a specific velocity over a particular period of time. These three concepts—velocity, distance, and time—are interconnected, as we have discussed. However, what happens to the body itself? The body possesses mass, which is a fundamental property of matter. According to Newton’s second law of motion, force is directly proportional to mass, and the constant of proportionality between them is acceleration. This implies that a body subjected to a constant force will experience an acceleration at a constant rate. In other words, its velocity will increase steadily (the velocity varies, but the acceleration remains constant). As a result, all bodies on Earth are attracted by a constant acceleration of approximately 9.8 m/s². This viewpoint aligns with classical mechanics, which assumes absolute space and varying velocities. However, from the perspective of relativity, if the rate of acceleration continues to increase, it would eventually surpass the speed of light. This is not possible, as the constancy of the speed of light has been established in the universe. Therefore, just as the dimensions of space and time are affected by velocity, the mass of an object also depends on its velocity. As an object’s velocity increases, so does its mass.
But how does mass increase? Does this mean that new atoms are added to matter? What is the source of this increase?
Certainly, the increase does not occur out of nowhere, as that would violate the principle of conservation of mass. The increase is not attributed to the physical properties of the body itself, but rather to a simultaneous increase in kinetic energy and mass. This increase is an inevitable result of the properties of the relative composition of space and time. In other words, a certain amount of matter can be converted into energy. This conversion occurs not only in the case of movement but even with static objects, which store a significant amount of energy. This includes both you and me, as well as the piece of sugar in your cup of tea.
Year of miracles:
Einstein’s ideas on special relativity were published in several papers, including one titled The Electrodynamic Movement of Bodies in September 1905. In addition, he wrote two scientific papers, one addressing “the principle of the photoelectric effect” and the other discussing “the Brownian movement of matter.” The journey that led Einstein to formulate the theories of special and general relativity was marked by social, emotional, and political drama. It involved encounters with racism and a struggle against the scientific community’s initial rejection of his ideas. The first season of the television series Genius, produced by National Geographic in April 2017, discussed the life, ideas, and conflicts of this remarkable scientist, drawing inspiration from the book Einstein: His Life and Universe by Walter Isaacson.
The theory of special relativity can be summarized as follows:
- All laws of physics are consistent and applicable in all frames of reference.
- The speed of light in a vacuum remains constant and is unaffected by the motion of the source or observer.
- Objects in reference frames moving at speeds close to the speed of light experience a contraction in length along the direction of motion.
- Time dilates in reference frames that move at speeds close to the speed of light.
- There is an equivalence between matter and energy, allowing for their conversion from one form to another.
Upon examining the previous findings, two notable gaps become apparent:
- Relativity did not initially include an explanation for gravity, despite it being a fundamental concept in physics.
- If the speed of light remains constant, it implies that acceleration should be zero. However, in our everyday world, we observe objects such as trains, carts, and falling objects undergoing acceleration. How can the principles of relativity be applied in non-inertial reference frames?
In the early part of 1907, Einstein recognized the limitations of special relativity and subsequently renamed his research the Special Theory of Relativity. Over the course of four years, he grappled with the shortcomings of his theory, seeking to generalize it. It was during this time that he encountered a pivotal thought experiment: What if I were in an elevator descending at a rapid speed and it suddenly became free-falling? In such a scenario, I would experience a loss of the sensation of gravity and move freely within the elevator, akin to flying. Conversely, if the elevator malfunctioned while ascending and accelerated rapidly, I would find my feet pressed against the elevator floor.
We encounter a similar sensation when riding a roller coaster at an amusement park. As the coaster ascends, we feel firmly seated, and during the rapid descent, it feels as though we might be propelled out of our seats and pressed against the safety harness. Understanding relativity provides a solution to this puzzle. The key lies in recognizing that my presence within the elevator aligns me with a particular frame of reference. Both the elevator and I experience the same rate of acceleration during free fall, effectively nullifying the influence of gravity. This is why astronauts are able to move freely inside their spacecraft; their acceleration matches that of their vehicle, rather than gravity being absent in space.

Spacetime
Once we have grasped the concept of a new relative space, where the only constant is the speed of light and everything else varies across different frames of reference, we can appreciate the beauty of mathematics. On Earth, we exist within three dimensions of space and one dimension of time. When arranging a meeting with a friend, we specify the time and location, such as “five o’clock at the Relativity Café.” We don’t need to provide the coordinates of the place (x = 3, y = 4.5, z = 9), as that would only confuse matters and make it difficult for our friend to respond. However, when studying the motion of objects, we employ three-dimensional axes and consider time as the fourth dimension, employing calculus. In the equations of Galileo and Newton, time remains fixed and absolute in one direction. Let me explain further: Suppose you arrive at the café at five o’clock, and if your friend is like most of my friends, they might be half an hour or more late. In the state of stillness at the same location, the fourth dimension of time continues to elapse. For Galileo and Newton, time is absolute and “unidirectional.” However, in relativity, although you are relatively at rest in the three dimensions of space, you are constantly moving through the dimension of time at the speed of light. If you call your friend, frustrated by their tardiness, they might insist that they are in a hurry. Their increased speed comes at the expense of reducing their travel time. Instead of thinking of time merely as time, consider it as the fourth mathematical dimension within a four-dimensional space. You exist within the three dimensions of space, but in the dimension of time, you move at the speed of light. Meanwhile, your friend may be moving at a speed of 80 miles per hour in the dimensions of space, but in the dimension of time, their speed is less than the speed of light. Their focus on moving through the dimensions of space comes at the cost of reduced speed in relative space, resulting in a speed lower than that of light. Treating time as the fourth dimension and employing its equations is the creative insight of the great mathematician Minkowski, drawing upon the geometry of Lobachevsky and Gauss. These four dimensions collectively form the fabric of space-time, shaping our understanding of movement in the universe.
In Euclidean geometry, which describes flat space in two dimensions, the sum of the angles in a right triangle is 180°. However, when we move to non-Euclidean geometry, which describes curved spaces, the laws of geometry change drastically. In such spaces, like a curved surface, the sum of the angles in a right triangle can be different from 180°. For example, in certain curved spaces, the sum may be 230°. However, when it comes to studying space-time, we require a four-dimensional space known as geodesic space. In this context, the sum of the angles in a right triangle within this four-dimensional space becomes 270°. Exploring the mathematical intricacies of these spaces is beyond the scope of this discussion. Nonetheless, studying these spaces helps us understand how space-time can be curved by the presence of mass. Every object, regardless of its size, contributes to the curvature of space-time, although the effect of curvature caused by small objects is usually minimal and can be considered negligible in many cases.

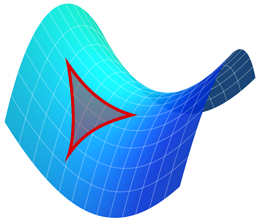
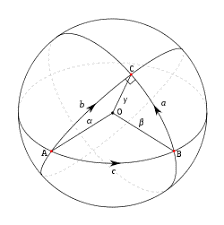
To simplify our understanding of the fabric of spacetime, we will use the concept of the light cone, as illustrated in the following figure:
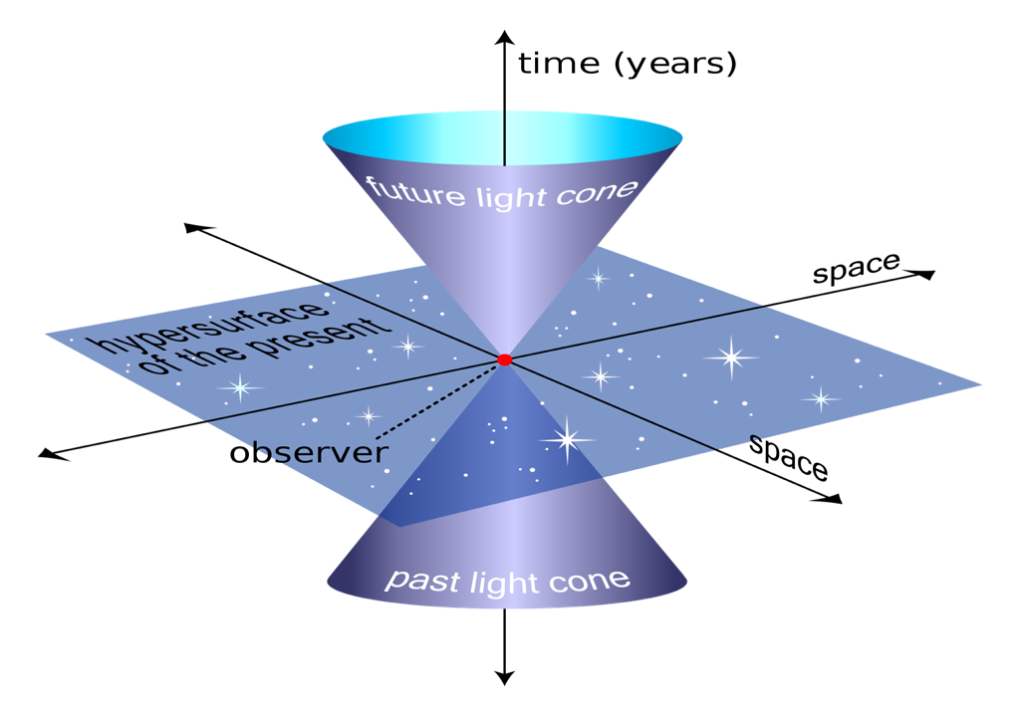
The red dot represents an event happening in the present, let’s say an explosion on planet Earth. Light, which is electromagnetic radiation, propagates in all directions like waves, similar to the ripples expanding on the surface of a lake over time, eventually creating a cone, with the red dot as its head, representing the moment of the explosion, as it expands into space. As the light waves travel through space, they will reach various locations at different times. For instance, if there were a spacecraft positioned at the outer edge of our solar system, it would observe the event several hours later, depending on the distance between Earth and the spacecraft. This would correspond to the upper cone in our visualization. On the other hand, if a massive explosion occurred on Jupiter’s surface, the light waves would spread through space until they reach our eyes in the present moment, forming the lower cone in our representation. Now, let’s consider a scenario where a black hole in our galaxy swallows the entire Milky Way. On a planet located thousands of light years away in a different galaxy, there might be sentient beings observing us. From their perspective, our beautiful galaxy—assuming it hasn’t been consumed by a black hole—would still be shining brightly in their sky. The present for us becomes the future for the inhabitants of that distant galaxy. This leads us to the same examples of time dilation as discussed previously.
How can we be rebuked for the nostalgic yearning for the past with the humbling realization that when we gaze upon the cosmos, we are merely witnessing the distant echoes of a long-gone past?!
Gravity and the curvature of space-time:
Do you recall the mock elevator experiment? For the sake of this discussion, let’s imagine that there is no gravity and that there is a flashlight positioned on the right side of the elevator. This flashlight emits a beam of light, as depicted in the diagram below. Now, if there is an observer watching the event from outside the elevator, under conditions where there is no acceleration (meaning the elevator is either stationary or moving at a constant speed), the light will travel in a straight path, similar to the left side of the picture. However, if the elevator is moving upward and experiences acceleration, the light will actually bend, as shown on the right side of the picture.
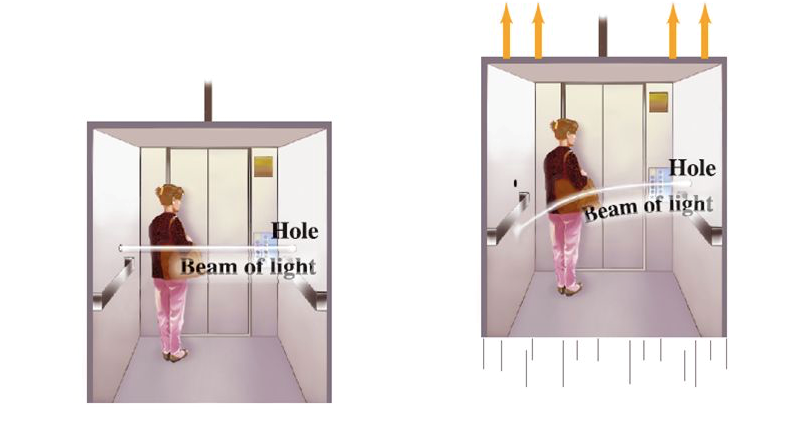
Let’s revisit Galileo’s statement: “In the absence of air resistance (the force of friction), all objects fall with the same acceleration.” This principle is known as the “principle of equivalence.” It implies that the gravitational mass is equivalent to the inertial mass. To explain the phenomenon of light bending based on the principle of equivalence, consider the scenario where an elevator is moving upward with an increasing vertical velocity relative to the light. In this case, an upwardly accelerating frame of reference can be seen as equivalent to an inverse gravitational field, resulting in the bending of the light ray. Understanding this particular point forms the core of general relativity, which asserts that gravity affects light and causes its deflection. By observing the light emitted by stars in the night sky, we can straightforwardly test the validity of general relativity using this concept.
Does the sun’s gravity cause light to deflect?
To validate the accuracy of general relativity, it is necessary to conduct experiments in space since the bending of light is primarily influenced by massive celestial bodies such as stars (like the Sun) and black holes. Prior to the development of the theory of relativity, our knowledge of gravity was limited to the gravitational pull exerted by the closest star, the sun. If general relativity holds true, the light emitted by stars, as observed from our vantage point on Earth, should experience a slight deflection of approximately 1.75 arc seconds near the outer edge of the sun. Although this deflection is minimal, it holds significant implications. However, due to the interference caused by sunlight, direct observation of starlight becomes possible only during a total solar eclipse. This circumstance prompted the British scientist Arthur Eddington to observe this phenomenon.
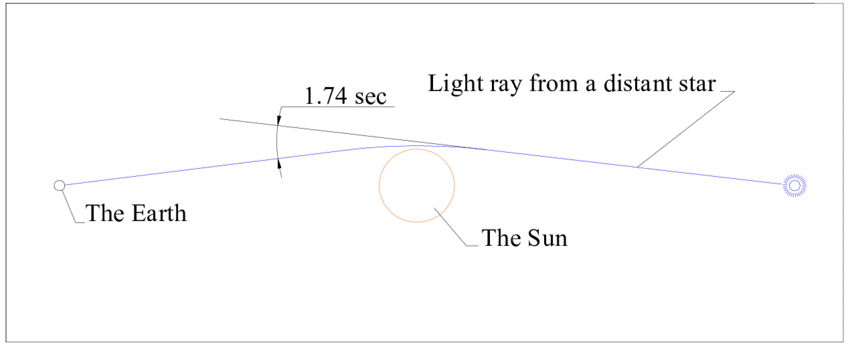
The eclipse that propelled Einstein to fame
Exactly a century ago, on May 29, our perception of the universe underwent a transformative shift. The disciplines of relative mathematics and physics were forever altered, and an individual would ascend to become the most renowned figure in history. During that momentous day, Albert Einstein found himself in his Berlin home office, engrossed in correspondence with his mathematician friend, Theodor Kaluza. Their exchange revolved around a space-time quandary that necessitated the consideration of five dimensions. Little did Einstein anticipate that his name and visage would soon grace every corner of the globe.
The Royal Society in London had enlisted the services of Arthur Eddington, the most distinguished metrologist then, to investigate novel astronomical theories. As fate would have it, Eddington chanced upon Einstein’s preliminary work on relativity and resolved to test the theory’s validity. The backdrop of World War I, combined with the prevailing sentiment in England to combat not only German Caesarism, but also German science, played a role in Eddington’s endeavor. Particularly noteworthy was a collective declaration of support for the war by a group of German scientists. Eddington faced financial challenges in securing funding for his expedition due to the aftermath of a German poison gas attack that exposed 1,500 English soldiers. Persuasively, Eddington argued to the Society, “If our experiment disproves Einstein’s theory, Newton’s legacy remains secure, and English science maintains its standing. However, if relativity proves true, England will have missed an opportunity to be at the forefront of this groundbreaking event.”
On May 29, 1919, an opportune total solar eclipse was set to occur, offering only two viable observation locations: Sobral in Brazil and the island of Príncipe off the west coast of Africa. Two exploratory missions were dispatched, armed with cameras to capture the eclipse and subsequently compare the images with those of the night sky’s star positions. Upon their return to London, the photographs were meticulously examined, revealing the preserved evidence of light deflection due to the Sun’s gravitational pull. Einstein received the preliminary results in September and jubilantly wrote to his mother to inform her of the “good news,” even treating himself to a new violin. The official confirmation was announced in November at the Royal Astronomical Society, igniting a wave of excitement that rippled through the headlines.


News about proving general relativity in international newspapersGeneral relativity triumphed at last, and with this great discovery, the foundations of absolute space crumbled, reshaping our perception of the universe. Similar to Galileo’s pivotal act of directing his telescope skyward in 1609, which debunked the notion of Earth as the center of the cosmos, general relativity elevated our understanding and contemplation of existence. Presently, countless telescopes worldwide peer into the vastness of space, unraveling its narrative. It is a narrative that exposes the folly of human arrogance, encapsulated by our disputes, wars, differences, and ceaseless quest for truth versus falsehood, right versus wrong, and the binary distinctions of white and black. In this pursuit, we often overlook that “within the gray reside many nuanced possibilities.”

T1607







